At a Glance:
- Advanced Models for Complex Data: Ridge, Lasso, and Elastic Net address issues like multicollinearity and non-linearity that basic linear regression can't handle.
- Real-World Impact: Regression goes beyond theory, predicting economic trends, stock prices, and more.
- Choosing the Right Tool: Each model fits unique data needs, making it accurate and insightful for predictive analysis.
What is Linear Regression?
Linear regression is a statistical method that predicts a variable's value based on another variable's value. The variable whose value is being predicted is the dependent variable, while the variable used to indicate the value is an independent variable.
For example, if a graph is plotted, the x-axis will have the independent variable while the y-axis will be dependent, as the values on the x-axis will be used to find the y-axis values. If the graph is plotted to form a straight line, then both the x and y values will have a linear relationship.
Limitations of Linear Regression
Linear Regression Models are useful but some limitations can make them redundant and inaccurate. It can be used on simpler values or relationships. However, issues like collinearity, outliers, and correlation of errors can occur when using complicated linear models. Linear regression models are sensitive to outliers and noise. Outliers are data points that do not lie on the same path as the rest of the dataset and noise is the error in the dataset. Linear regression models do not account for these. This can make the results inaccurate.
It is important to use scatter plots, z-scores, and histograms to examine the data before using it in predictive analysis. Overfitting and underfitting also affect regression models negatively. While overfitting does take noise into account, it does not work properly on new data. Similarly underfitting is when the data does not fit on the regression model. To correct it, fitting selection and engineering techniques are important.
However, the relationship between two variables cannot always be linear. It can be non-linear and drawn as a curve rather than a straight line.
Beyond Linear: Polynomial regression
Polynomial regression is an extension of linear regression that captures the nonlinear relationship between a dependent and independent variable. It can handle more complex patterns to measure the nonlinearity using the mean and R- R-squared functions. The independent variable x and the dependent variable y are modeled as an nth-degree polynomial in x. This can also be used to analyze stock prices.
Multicollinearity occurs when two or more independent variables show a high correlation. This means that the regression coefficients are unstable and can not be predicted. To avoid multicollinearity, there is no linear dependence between the predictors. It occurs when one variable is a multiple of another variable.
In this case, since the variables are perfectly correlated, one variable explains 100% of the other variable and there is no added value to take both variables in a regression model. If there is no correlation between the independent variables, then there is no multicollinearity.
Addressing Multicollinearity: Ridge and Lasso Regression
Ridge regression is specifically used to avoid multicollinearity in the data set. Linear regression does not provide reliable and stable estimates. It prevents overfitting by penalizing large coefficients with a regularization term, L2 penalty. This usually helps shrink the sum of squared coefficients bringing it closer to zero. On the other hand, Lasso regression sets some coefficients to zero. It uses feature selection to bring inefficient variables to zero while also reducing storage and processing requirements.
Elastic Net: A Balanced Approach for Complex Datasets
Elastic net is a regression technique that helps to handle multicollinearity and inefficient coefficients simultaneously. It combines Ridge and Lasso Regression to balance complex datasets. It offers flexibility by controlling the ratio between ridge and lasso regression.
Elastic net provides a solution to these problems. It performs well across different types of datasets.
Logistic regression is structurally similar to a linear regression model but is mostly used to classify continuous data rather than for predictive analysis. It has a binary outcome and is used to find a relationship between two data factors. This type of regression uses one data value to predict the value of the other. The outcome mostly has a finite value. It can also be said that it estimates the probability of an event occurring. Like, if a customer will purchase a commodity (yes/no).
There are many nonlinear alternatives to linear regression models. Nonlinear regression models help to capture complex relationships between the parameters. It can be useful for real-world factors like economics, by helping to predict stock prices, interest rates, and much more.
Support Vector Machines
Support Vector Machines are flexible and nonlinear alternatives that classify data and perform predictive analysis. They capture complex relationships that are impossible for linear models. SVM predicts and classifies data by finding a hyperplane that maximizes the distance between each class in an N-dimensional space.
The number of factors in the input data determines if the hyperplane is in a 2-D space or a plane in a n-dimensional space. Maximizing the margin between points enables the algorithm to find the best decision boundary between classes since multiple hyperplanes can be found to differentiate classes. This helps train new data and make accurate classification predictions. The lines that are adjacent to the optimal hyperplane are known as support vectors. It is because these vectors run through the data points that determine the maximal margin.
Decision Trees and Random Forests
Decision trees make predictions based on well-crafted questions. The algorithm trains the data set and models it on a tree. An ML algorithm generates and trains the given tree based on the provided dataset. This training consists of choosing the right questions about the right features placed in the right spot on the tree.
The algorithms can work with categorical and numerical data while producing classification and regression trees as well. The names of popular models are ID3, C4.5, CART, CHAID, and MARS. The simplicity of decision trees makes them useful. A collection of many decision trees makes random forests. It is efficient and easier to classify and train data. The trees in a random forest are correlated making them a part of the larger data analysis.
Principal Component Regression (PCR):
Principal Component regression is a technique based on Principal Component Analysis. It estimates the unknown regression coefficients in a standard linear regression model. It is a combination of multiple linear regression and principal analysis. It reduces the number of independent variables, also known as predictor values, for future analysis. When running PCR from PCA, choosing the outcome or dependent variable that differs from the input is important. PCR reduces multicollinearity between two or more of the independent variables.
.png)
K-Nearest Neighbors Regression
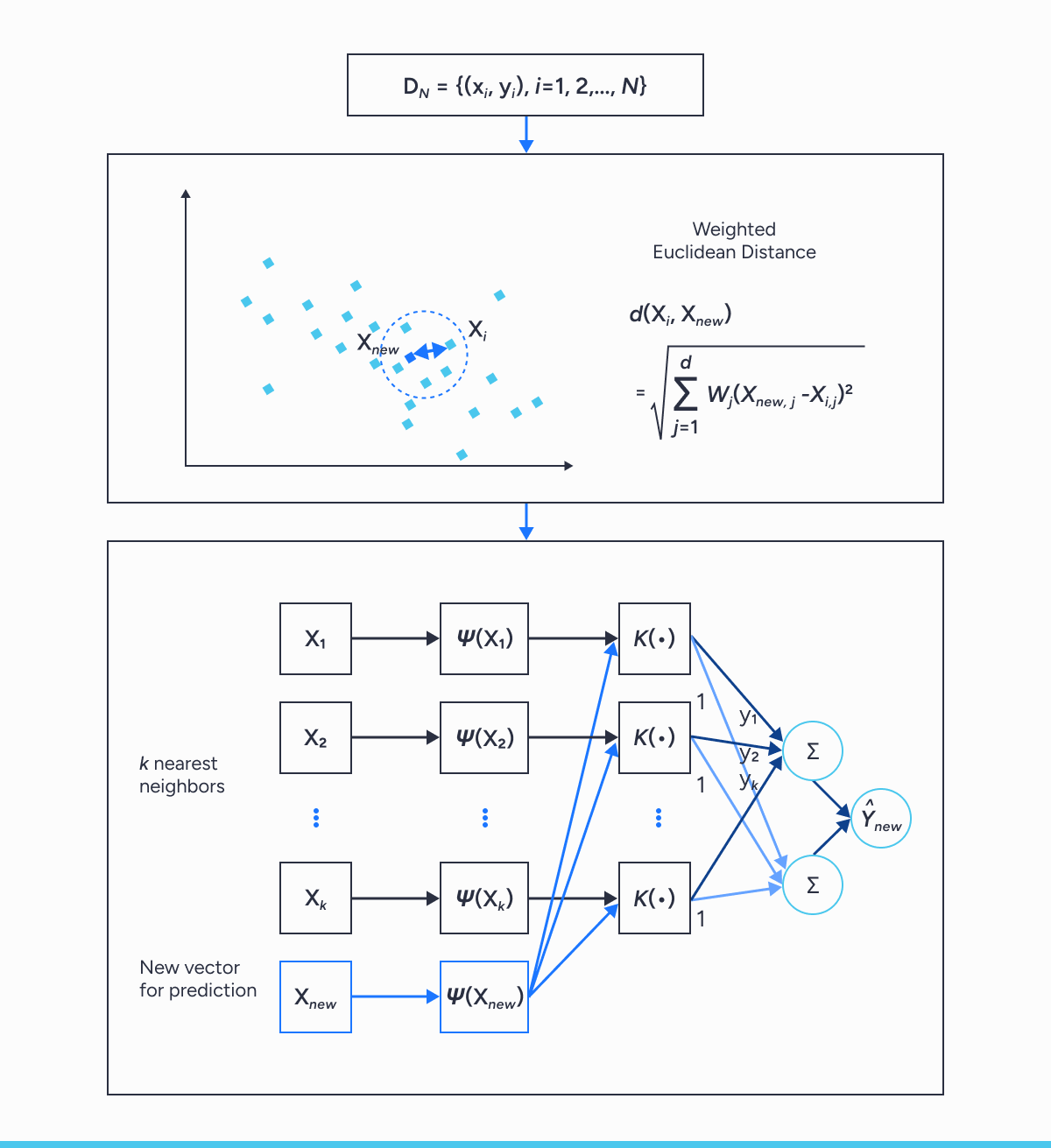
K-Nearest Neighbors Regression is a supervised learning algorithm used for classification and regression. KNN predicts the correct class for the test data by calculating the distance between the test data and all the training points. Then select the K number of points closest to the test data. It makes predictions by assigning a new data point to the majority set within its neighbors as a classification algorithm. However, as a regression algorithm, kNN predicts results based on the average values closest to the query point. During classification, individual test samples are compared locally to k neighboring training samples in variable space, and their category is identified according to the classification of the nearest k neighbor.
Understanding and Measuring Change in the Economy
Regression models, including linear regression, are powerful tools to measure economic shifts. They help predict future trends and the rate of change (derivative) by analyzing historical data within an economic or business environment. For example, businesses can use regression to measure how changes in interest rates impact consumer spending or assess how shifts in employment levels influence GDP. The ability to quantify the rate of change is essential for companies making data-driven decisions in dynamic markets. The best measure of the economy is Gross Domestic Product (GDP). Future GDP can be analyzed through the linear regression model. However, the analysis may involve other factors like Interest rate, consumer spending, Gross National Income, Inflation, etc. This can complicate the model so it will be better to use different forms of regression like polynomial, ridge, lasso regression, etc.
Final Thoughts: Selecting the Right Regression Model
Linear regression remains a foundational method, but its alternatives expand analytical options to fit diverse datasets. For data scientists and analysts, choosing the right model is essential to ensure accurate predictions that drive actionable insights. Linear regression models only sometimes work accurately for practical data in science or economics. This is due to the complex nature of the parameters or the amount of data used to analyze future trends. There are many issues that linear regression needs to account for due to its simplicity. These issues can cause major variances, biases, or errors in the output values. Thus, it is important to use the alternative models listed above considering the nature of the data being analyzed. These models help to predict accurate results that are helpful in practical usage.
